Phân Bố Là Gì? Khái Niệm, Loại Phân Bố & Ứng Dụng Thống Kê
Phân phối là gì? Câu hỏi này nghe có vẻ đơn giản nhưng trên thực tế khái niệm phân phối vô cùng rộng và có thể áp dụng trong nhiều lĩnh vực khác nhau. Từ việc hiểu phân bố dân số, đến phân bổ ngân sách của một công ty, đến phân bổ xác suất trong thống kê hoặc phân bổ tần suất dữ liệu, tất cả đều liên quan đến khái niệm cơ bản này.
Bài viết này của KTH GARDEN sẽ giúp các bạn hiểu rõ hơn về phân phối, tìm hiểu các loại phân phối khác nhau như phân phối chuẩn, tìm hiểu cách sử dụng biểu đồ để trực quan hóa dữ liệu phân tán, cũng như cách áp dụng Phân tích phân phối vào thực tế thông qua các phân bổ cụ thể, dễ hiểu. ví dụ. Bạn sẽ làm quen với các mô hình phân phối, tìm hiểu cách sử dụng phần mềm thống kê và hiểu tầm quan trọng của việc phân tích dữ liệu phân tán trong việc ra quyết định.
Phân phối là gì? Các khái niệm cơ bản và các loại phân phối
Phân phối, trong bối cảnh thống kê, đề cập đến cách dữ liệu được trải rộng hoặc phân chia trên một phạm vi giá trị nhất định. Nó cho chúng ta biết tần suất của từng giá trị hoặc nhóm giá trị trong tập dữ liệu. Hiểu phân phối là nền tảng để phân tích dữ liệu hiệu quả và đưa ra quyết định chính xác dựa trên dữ liệu. Hãy hình dung nó như một bức tranh, cho thấy mức độ “tập trung” hoặc “phân tán” của các điểm dữ liệu. Ví dụ, sự phân bố dân cư cho biết số lượng người sống ở từng khu vực địa lý, giúp chính phủ lập kế hoạch quy hoạch đô thị và phân bổ nguồn lực hiệu quả hơn. Một ví dụ khác là phân bổ ngân sách, thể hiện số tiền được phân bổ cho từng dự án, giúp đảm bảo tính hiệu quả và minh bạch trong quản lý tài chính. Khái niệm này có ứng dụng rộng rãi, từ kinh tế, xã hội đến khoa học tự nhiên.
Một trong những khía cạnh quan trọng nhất của việc hiểu phân phối là phân biệt giữa các loại phân phối khác nhau. Không phải tất cả dữ liệu đều được phân phối như nhau. Sự khác biệt về hình dạng và đặc điểm của việc phân bổ dữ liệu sẽ dẫn đến các phương pháp phân tích khác nhau. Ví dụ: một số dữ liệu có thể tuân theo phân phối chuẩn, có hình chuông đặc trưng, trong khi các dữ liệu khác có thể có phân phối lệch phải hoặc trái, biểu thị mức độ tập trung dữ liệu không đồng đều. Hiểu được loại phân phối giúp lựa chọn phương pháp thống kê phù hợp để phân tích và đưa ra kết luận chính xác.
Các loại phân phối dữ liệu thống kê phổ biến
Có nhiều loại phân phối dữ liệu thống kê, mỗi loại có những đặc điểm riêng. Việc lựa chọn kiểu phân phối phù hợp sẽ quyết định độ chính xác của kết quả phân tích. Dưới đây là một số kiểu phân phối phổ biến:
Phân phối chuẩn: Đây là một trong những loại phân phối được sử dụng nhiều nhất trong thống kê. Nó có hình dạng đối xứng, hình chuông, với hầu hết dữ liệu tập trung xung quanh giá trị trung bình. Đặc tính này được mô tả bằng các tham số trung bình (μ) và độ lệch chuẩn (σ). Nhiều hiện tượng tự nhiên tuân theo sự phân bố này, ví dụ như chiều cao của con người trong dân số.
Phân phối nhị thức: Loại phân phối này được sử dụng khi xem xét một loạt các thử nghiệm độc lập với hai kết quả có thể xảy ra (thành công hoặc thất bại), mỗi thử nghiệm có xác suất thành công hoặc thất bại. thay đổi. Ví dụ: nếu bạn tung đồng xu 10 lần, xác suất xuất hiện 3 mặt ngửa sẽ được tính bằng phân phối nhị thức. Số lần thử (n) và xác suất thành công trên mỗi lần thử (p) là hai tham số chính xác định phân phối này.
Phân phối Poisson: Loại phân phối này mô tả số lượng sự kiện xảy ra trong một khoảng thời gian hoặc không gian xác định, khi tốc độ xảy ra sự kiện là không đổi. Ví dụ: số lượng khách hàng ghé thăm cửa hàng trong một giờ nhất định hoặc số lỗi in trên một trang sách. Tham số chính là λ (lambda), biểu thị tốc độ trung bình xảy ra sự kiện. Một ví dụ điển hình về phân phối Poisson ngoài đời thực là số lượng ô tô đi qua một điểm trên đường cao tốc trong một khoảng thời gian nhất định. Giả sử trung bình có 100 ô tô đi qua mỗi giờ, chúng ta có thể sử dụng phân phối Poisson để tính xác suất có 120 ô tô đi qua trong một giờ cụ thể.
Phân phối đồng đều: Trong kiểu phân phối này, tất cả các giá trị trong một phạm vi được chỉ định đều có xác suất xuất hiện như nhau. Ví dụ: tung xúc xắc công bằng sẽ tạo ra sự phân bố đồng đều từ 1 đến 6.
Việc lựa chọn loại phân phối nào phụ thuộc vào bản chất của dữ liệu và mục đích của nghiên cứu. Một sai sót trong việc lựa chọn phân phối sẽ dẫn đến kết quả phân tích không chính xác và đưa ra quyết định không hiệu quả. Sự hiểu biết sâu sắc về các loại phân phối là rất quan trọng đối với một nhà phân tích dữ liệu.
Phân tích dữ liệu và thể hiện phân phối dữ liệu
Sau khi thu thập dữ liệu, bước tiếp theo là phân tích và biểu diễn phân bổ dữ liệu để hiểu rõ hơn về tập dữ liệu. Có nhiều phương pháp để phân tích và biểu diễn phân bố dữ liệu, tùy thuộc vào loại dữ liệu và mục đích nghiên cứu.
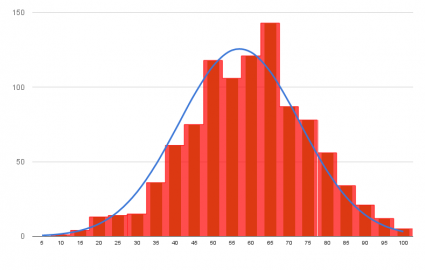
Một trong những công cụ cơ bản là biểu đồ. Các loại biểu đồ như biểu đồ, biểu đồ và đường cong phân phối cho phép chúng ta hình dung cách phân phối dữ liệu. Biểu đồ chia dữ liệu thành các khoảng (thùng) và hiển thị tần suất dữ liệu trong mỗi khoảng. Biểu đồ liệt kê các giá trị dữ liệu và tần suất xuất hiện của chúng. Đường cong phân phối cho thấy xu hướng chung của phân phối dữ liệu. Việc lựa chọn giữa các loại biểu đồ phụ thuộc vào loại dữ liệu và thông tin bạn muốn truyền tải. Ví dụ: biểu đồ hữu ích cho dữ liệu liên tục, trong khi biểu đồ phù hợp hơn cho dữ liệu rời rạc. Ngoài ra, bảng dữ liệu phân bổ chi tiết sẽ giúp người đọc hiểu rõ hơn về dữ liệu gốc.
Bên cạnh việc sử dụng biểu đồ, các chỉ số thống kê mô tả như giá trị trung bình, trung vị, mode, độ lệch chuẩn, phương sai cũng được sử dụng để mô tả phân bố dữ liệu. Giá trị trung bình biểu thị giá trị trung bình của tập dữ liệu, trong khi trung vị biểu thị giá trị ở giữa khi dữ liệu được sắp xếp theo thứ tự. Chế độ cho biết giá trị xuất hiện thường xuyên nhất. Độ lệch chuẩn và phương sai đo lường độ phân tán của dữ liệu xung quanh giá trị trung bình. Ví dụ: nếu độ lệch chuẩn cao, điều đó cho thấy dữ liệu rất phân tán, trong khi đó, nếu độ lệch chuẩn thấp thì dữ liệu tập trung quanh giá trị trung bình.
Ngoài ra, các phần mềm thống kê như SPSS, R, SAS cung cấp các công cụ mạnh mẽ để phân tích và thể hiện phân bố dữ liệu một cách chi tiết, từ tính toán các chỉ số thống kê đến xây dựng dữ liệu. Biểu đồ phức tạp. Sử dụng những phần mềm này giúp tiết kiệm thời gian và tăng độ chính xác trong quá trình phân tích. Một số phần mềm còn có khả năng kiểm tra các giả thuyết về phân bố dữ liệu, giúp chúng ta xác định liệu dữ liệu có tuân theo một phân bố cụ thể hay không. Ví dụ: chúng ta có thể sử dụng thử nghiệm Kolmogorov-Smirnov để kiểm tra xem dữ liệu có tuân theo phân phối chuẩn hay không.
Ứng dụng phân phối thống kê trong thực tiễnCông cụ, phần mềm hỗ trợ phân tích dữ liệu phân phối Ví dụ minh họa phân phối trong thực tế
Với hơn 20 năm kinh nghiệm trong lĩnh vực phân tích dữ liệu, tôi nhận thấy việc hiểu và áp dụng phân phối thống kê không chỉ quan trọng trong nghiên cứu học thuật mà còn mang lại giá trị to lớn trong thực tiễn. Khả năng diễn giải dữ liệu thông qua các mô hình phân phối cho phép chúng tôi đưa ra quyết định chính xác hơn, tối ưu hóa nguồn lực và dự đoán xu hướng một cách hiệu quả.
Một trong những ứng dụng quan trọng nhất của phân phối thống kê là trong lĩnh vực kinh doanh. Ví dụ: các công ty sử dụng phân bổ để phân tích hành vi của khách hàng. Bằng cách thu thập và phân tích dữ liệu về thói quen mua sắm, sở thích sản phẩm và các yếu tố nhân khẩu học, doanh nghiệp có thể tạo ra các chiến lược tiếp thị hiệu quả hơn. Phân phối xác suất giúp dự đoán nhu cầu thị trường, tối ưu hóa quy trình sản xuất, quản lý kho hàng hiệu quả hơn và giảm thiểu rủi ro về hàng tồn kho. Ví dụ, một công ty thời trang có thể sử dụng kênh phân phối để dự đoán nhu cầu về các mẫu áo sơ mi mới trong mùa thu đông, giúp họ lên kế hoạch sản xuất và tìm nguồn cung ứng phù hợp, tránh tình trạng thiếu hàng hoặc tồn kho. quá nhiều.
Trong y học, phân bố thống kê có vai trò vô cùng quan trọng. Các nhà nghiên cứu sử dụng phương pháp phân phối để phân tích dữ liệu lâm sàng, đánh giá hiệu quả của các loại thuốc mới và xác định các yếu tố nguy cơ gây bệnh. Ví dụ, phân phối chuẩn được sử dụng rộng rãi để mô tả chiều cao và cân nặng của một dân số, từ đó giúp bác sĩ đánh giá tình trạng sức khỏe của bệnh nhân một cách khách quan hơn. Phân tích phân bố cho phép các chuyên gia y tế theo dõi sự lây lan của dịch bệnh, lập kế hoạch phòng chống dịch bệnh hiệu quả và đánh giá tác động của các biện pháp y tế công cộng. Phân tích dữ liệu về thời gian điều trị cũng được sử dụng để tối ưu hóa quy trình chăm sóc y tế.
Ứng dụng phân phối thống kê còn mở rộng sang các lĩnh vực khác như tài chính, bảo hiểm và kỹ thuật. Trong tài chính, phân phối giúp nhà đầu tư đánh giá rủi ro và lợi nhuận của khoản đầu tư. Trong bảo hiểm, phân phối giúp các công ty tính toán phí bảo hiểm dựa trên phân tích dữ liệu về xác suất xảy ra rủi ro. Trong kỹ thuật, phân phối được sử dụng để kiểm soát chất lượng sản phẩm, dự đoán thời gian hoạt động của máy và tối ưu hóa quy trình sản xuất. Ví dụ: một nhà máy ô tô có thể sử dụng hệ thống phân phối để kiểm tra chất lượng của các bộ phận, đảm bảo độ bền và an toàn của sản phẩm.
Để thực hiện những phân tích này, chúng tôi cần các công cụ và phần mềm thống kê mạnh mẽ. Các phần mềm như SPSS, R, SAS và Python (với các thư viện như SciPy, Statsmodels) cung cấp các công cụ và chức năng phong phú để phân tích dữ liệu, xây dựng mô hình phân phối và tạo biểu đồ. trực quan. Ví dụ: phần mềm R là một công cụ nguồn mở, linh hoạt và mạnh mẽ được sử dụng rộng rãi trong nghiên cứu thống kê và phân tích dữ liệu. Nó cung cấp nhiều thư viện và gói phần mềm để xử lý, phân tích và trực quan hóa dữ liệu, bao gồm các mô hình phân phối phức tạp. SAS, một phần mềm thương mại, nổi tiếng với khả năng xử lý lượng dữ liệu lớn và độ tin cậy cao, thường được sử dụng trong các tổ chức lớn.
Ví dụ minh họa: Hãy tưởng tượng một công ty điện thoại muốn phân tích sự phân bổ độ tuổi của khách hàng để thiết kế các chiến dịch tiếp thị phù hợp. Bằng cách thu thập dữ liệu từ cơ sở dữ liệu khách hàng và sử dụng phần mềm thống kê như SPSS, công ty có thể xây dựng biểu đồ để trực quan hóa sự phân bổ độ tuổi. Từ đó, họ có thể chia khách hàng thành các nhóm tuổi khác nhau và thiết kế các chiến dịch quảng cáo riêng biệt. Các nhóm khách hàng trẻ hơn có thể được nhắm mục tiêu bằng quảng cáo trên mạng xã hội, trong khi các nhóm khách hàng lớn tuổi hơn có thể được tiếp cận thông qua các kênh truyền thông khác.
Trên thực tế, việc sử dụng các công cụ phân tích phân phối thống kê và hiểu cách diễn giải kết quả mang lại hiệu quả kinh tế vượt trội. Tối ưu hóa quy trình, giảm thiểu rủi ro và đưa ra quyết định kinh doanh chính xác hơn đều dựa vào sự hiểu biết sâu sắc về dữ liệu và cách phân phối dữ liệu. Đây là một trong những lý do tại sao việc hiểu phân phối thống kê ngày càng trở nên quan trọng trong mọi lĩnh vực của cuộc sống.

 0934.19.6789
0934.19.6789